Two-part Addresses and Memory Segmentation
Memory addressing is the centerpiece of the memory management function of an operating system. Early systems had flat memory models in which each byte was numbered sequentially from zero. The address of any byte in memory was in effect just the ordinal number telling "which" byte it was, e.g., the seven hundred twenty-third or the forty-three thousand two hundred ninth. Programmers referred to each byte by its sequence number in their programs. These numbers are called "absolute" or "physical" addresses. Computers later became more complicated (in order to get more powerful). One change was that within programs, programmers could refer to memory locations (particular bytes) by other numbering systems than the physical one, and the operating systems and/or CPUs would automatically translate from one to the other.
Vintage 1980 microcomputers used physical addressing, and confined themselves to using 4-digit hexa numbers as addresses. The highest you can count with a 4-digit hexadecimal number is FFFF in hex, equivalent to 65535 in decimal. So no more than 65536 bytes or 64K of memory could be used. Even if you could have installed more, the computer could not have used it for lack of ability to refer to it.
The IBM designers wanted to allow for 1MB of memory, or 16 times as much as the previous 64K limit. But because they had all registers only 16 bit that is 2 bytes they did not wish to use numbers wider than 16 bits in their addressing system. So a system of compound addresses. Each compound address contained 2 16-bit numbers. These were the first "segmented addresses" in microcomputers and the second one called as the offset address.
To understand this in a better way let me lead with an example in decimal. Forget hexadecimal, and computers, for a moment. In decimal we'll do the same thing that the 1981 PC architects did. Suppose till now we have been content to confine ourselves to counting using 2-digit numbers. Of course, that gave us the scope to count within the range from zero to ninety-nine. That has always been adequate. Ninety-nine is enough. It really has never occurred to us to count any higher.
Now however, an ambitious engineer wants to do just that. He knows he can do it if he allows a third digit. That gets us beyond the 99 barrier alright, not only to 100 but all the way up to the unimaginably huge number 999. For design reasons though, the engineer chooses to avoid using 3-digit numbers. Instead he opts to invent a system of compound numbers, consisting of 2 ordinary 2-digit number and a special way of interpreting them.
On the number line he will mark all numbers that are multiples of 10, starting with 0. Then he will use his first 2-digit number to identify a particular "deci-mark" on the number line. If his 2-digit number is 00 he's talking about the mark at 0. If it's 01, the mark at 10. If it's 02, the mark at 20,..., if it's 09, the mark at 90. If it's 10, the one at 100. If it's 11, the one at 110. If it's 25, he means the mark at 250. Since his 2-digit numbers go up to 99 before they run out of gas, he now has a technique of referring, as the limit of his reach, to the point at 990 on the number line. What he has sacrificed is the ability to refer to any of the "in-between" numbers, like 11 or 19 or 255. He has diluted his 2-digit number so it goes farther. He gained scope at the expense of precision. That's the purpose of the second 2-digit number: to supply restored precision.
Say he wants to refer to the number 763. He could select, as his first 2-digit number, 76. Because of the special, new "times ten" method of interpretation, we know this refers to the number 760. So he constructs a second 2-digit number to get him the rest of the way from 760 to 763. And that number is of course 3, which we'll write 03 to make it 2 digits. His notation system calls for him to write:
76:03
when he wishes to talk about 763. He now has a way to talk about it, but has successfully avoided using 3-digit numbers. Note he could land on 763 several other ways. For example, by starting at 750 instead of 760, then advancing 13 instead of 3. Just as the 43 yard line on the gridiron is equivalently a 3 yard gain from the 40, a 13 yard gain from the 30, or a 23 yard gain from the 10. All, same thing. So our engineer could write any of the following to refer to 763:
76:03
75:13
74:23
73:33
72:43
71:53
70:63
69:73
68:83
67:93
That's it. He can't let his first number go any lower than 67, because that would leave him short of 763 by more than 99, and the second number can only raise him 99 beyond his first one. You can make up the following rule for converting one of these compound addresses into a non-compound (i.e., regular 3-digit) one: to find the 3-digit linear address, take the left number of the compound address, shift it left one place (i.e., multiply it by 10), then add the right number.
The PC architects did pretty much the same thing. Instead of starting with 2-digit decimal numbers that provide a range of up-to-99, they started with 4-digit hex nos.providing a range of up-to-65536. But they compounded their numbers just the same way. And they ended up with an expanded reach. Their new reach, instead of extending up to 999 (just about a thousand), extended up to 1048575 ( just about a megabyte). But the system was the same. Consider an address 8F11:312A. The interpretation of this compound address and resulting absolute address is:
Note the above arithmetic is hexadecimal arithmetic, not decimal arithmetic. And note the result, 9223A, is much bigger than is FFFF, the previous counting ceiling. The two numbers have names. The left one is the segment address, and the right one is the offset address. Using this system to refer to memory locations is called memory segmentation. It's a way of making two 4-digit (hexadecimal) numbers do the work of one 5-digit number.
This was the new style of addressing by IBM's 1981 PC architects. Meanwhile, Intel's CPU designers made their own contribution. They came out with a chip (the 8086) that featured some new registers called segment registers. Programmers would work with the two-part addresses by doing two things within their programs. When they wanted to use a certain address, they would first take the segment address half of it and write it into the segment register. Thereafter, they would forget about the segment and write only the offset addresses within their code. They could get away with leaving out an explicit segment in all their address references due to the way the CPU worked. It was designed to blend (add) with the programmer's offset addresses whatever number was sitting in the segment register. And to do it every time there was an address reference, automatically. The segment address wasn't really omitted from the code, just implicit.
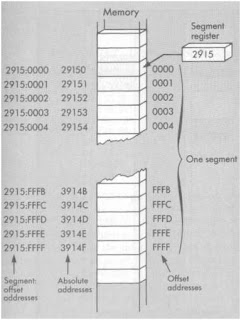
When you as a programmer put a number in a segment register you have in effect defined something called a "segment." This is a section of memory 64K bytes long. If the segment address is, for example, 2915, then the addresses in this segment start at 2915:0000 and go up to 2915:FFFF, which is the highest address in this particular segment. This range expressed in terms of absolute or physical addresses is from 29150 through 3914F. The relationship between a segment and the register which defines it is shown below.





0 comments:
Post a Comment